| ■適当講座■ 9.花子でCAD −図形の基礎− |
| a.図形の名称と特徴 | b.図形の各部の名称 | c.図形の性質 | d.三平方の定理 |
| e.立体の名称と特徴 | f.三角関数 | g.多面体 | h.曲面 |
| i.陰影 | j.透視 | k.角のn等分法 | l.曲線と直線 |
| f.三角関数 |
| あ)余弦と正弦 い)角度の表し方 う)θの三角関数に変形する公式 え)三角形への応用 | |
| え) 三角形への応用 |
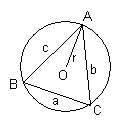
| 公式 正弦定理 △ABCにおいて、辺BC、CA、ABの長さがそれぞれa、b、cとすると a/(sinA) = b/(sinB) = c/(sinC) = 2r (rは△ABCの外接円の半径) |
 |
| 余弦定理 △ABCにおいて、辺BC、CA、ABの長さがそれぞれa、b、cとすると a2 = b2 + c2 - 2bc cosA b2 = c2 + a2 - 2ca cosB c2 = a2 + b2 - 2ab cosC |
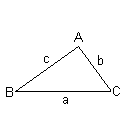 |
| 三角形の面積 △ABCの面積Sは2辺と夾角があきらかなとき、 S = 1/2(bc sinA) = 1/2(ca sinB) = 1/2(ab sinC) |
 |
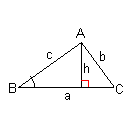
| 参考その他 三角形の面積 S = 1/2(ah) また、 h/c = sinB h = c sinB ヘロンの公式 S = [ s (s-a) (s-b) (s-c) ]1/2 ただし、 s = ( a + b + c ) / 2 |
 |
| 原点を中心とする回転 任意の点(x , y)を、原点を中心として反時計方向にθ の回転を行い、 (x' , y')の座標となるとき、 x' = x cosθ - y sinθ y' = x sinθ + y cosθ 任意の点(x , y)を、原点を中心として時計方向にθ の回転を行い、 (x' , y')の座標となるとき、 x' = x cosθ + y sinθ y' = - x sinθ + y cosθ 任意の点(xP , yP)を中心とした移動 X = x - xP X' = x' - xP Y = y - y' Y' = y' - yP と置換することにより、原点を中心とするケースに当てはめることができる。 |
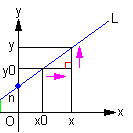
| 直線の方程式 傾きがm、y切片(y軸との呼応点)がnの直線の方程式は、 y = mx + n 点(x0 , y0)を通り、傾きがmの直線上に任意の点(x , y)をとれば、 = m(mは一定) 直線の方程式は、 y - y0 = m(x - x0) 2直線y = mx + n、 y' = m'x' + n'について、 平行条件 m = m' 直行条件 mm' = -1 |
 |
| ←前(三角関数-θの三角関数に変形する公式)へ | ここ(三角関数-三角関数の応用) | →次(多面体)へ |
| ▲このページトップへ |
| Copyright(C) KinutaHandicraft |