| ■適当講座■ 9.花子でCAD −図形の基礎− |
| a.図形の名称と特徴 | b.図形の各部の名称 | c.図形の性質 | d.三平方の定理 |
| e.立体の名称と特徴 | f.三角関数 | g.多面体 | h.曲面 |
| i.陰影 | j.透視 | k.角のn等分法 | l.曲線と直線 |
| f.三角関数 |
| 角度や辺の長さ、座標などを求めるとき三角関数が必要になります。 経験からいえば、直角三角形に基づく三角関数でこと足りますが、ここでは、知っておいた方がよいものについて紹介します。 |
|
| あ)余弦と正弦 い)角度の表し方 う)θの三角関数に変形する公式 え)三角関数への応用 | |
| あ) 余弦と正弦 |
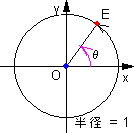
| 右図のxy平面で原点Oを中心として単位円(半径1の
円を単位円という)上の点Eの座標を考える。 点Eのx座標は、x = cosθ (余弦) 点Eのy座標は、y = sinθ (正弦) |
 |
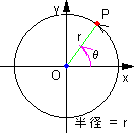
| ここで単位円の半径をr倍し、憧憬をrとした場合
(r > 09)、xy平面で原点Oを中心とした円上の点Pをを考える。 点Pのx座標は、x = r cosθ 点Pのy座標は、y = r sinθ そこで、以下の式が成り立つ。 cosθ = x / r (余弦) sinθ = y / r (正弦) tanθ = y / x (正接) |
 |
| つまり、覚え方としては、次のようになります。 |
| cosθ(コサイン・シータ、余弦) は、 筆記体のcを描く様にして、分母r、分子xになり、x / r |
sinθ(サイン・シータ、正弦) は、 筆記体のsを描く様にして、分母r、分子yになり、y / r |
tanθ(タンジェント・シータ、正接) は、 筆記体のtを描く様にして、分母x、分子yになり、y / x |
|||
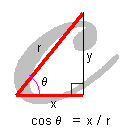
|
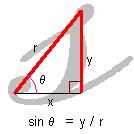 |
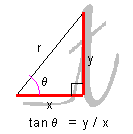 |
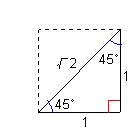
| 次に特別な直角三角形にsin/cos/tanを当てはめてみる。 |
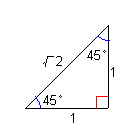 |
sinθ = 1 / (2)1/2 cosθ = 1 / (2)1/2 tanθ = 1 / 1 |
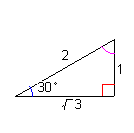 |
sinθ = 1 / 2 cosθ = (3)1/2 / 2 tanθ = 1 / (3)1/2 |
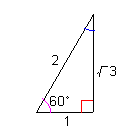 |
sinθ = (3)1/2 / 2 cosθ = 1 / 2 tanθ = (3)1/2 / 1 |
| 次の正方形、正三角形にも応用できます。 | |||
 |
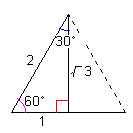 |
||
| ←前(立体の名称と特徴)へ | ここ(三角関数-余弦と正弦) | →次(三角関数-角度の表し方)へ |
| ▲このページトップへ |
| Copyright(C) KinutaHandicraft |