| ■適当講座■ 9.花子でCAD −図形の基礎− |
| a.図形の名称と特徴 | b.図形の各部の名称 | c.図形の性質 | d.三平方の定理 |
| e.立体の名称と特徴 | f.三角関数 | g.多面体 | h.曲面 |
| i.陰影 | j.透視 | k.角のn等分法 | l.曲線と直線 |
| d.三平方の定理 |
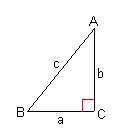
| 右図のように角(ACB)が直角である直角三角形ABCにおいて、
BC = a、AC = b、 AB = cとすると、次の関係が成り立つ。 a2 + b2 = c2 この定理を三平方の定理、またはピタゴラスの定理という |
 |
| 証明 | |
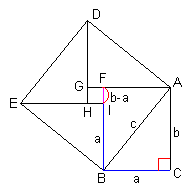
| 直角三角形ABCの斜辺ABを1辺とする正方形ADEBがあるとき、
この正方形の中には直角三角形ABCに等しい4つの三角形と、
これらの三角形に囲まれた正方形GHIFが入る。 すなわち、こららの5つの図形の面積合計と、正方形ADEBの面積は同じになる。 |
| ここで、直角三角形ABCに等しい4つの三角形の面積はいずれも (1/2)ab = 0.5ab であり、正方形GHIFの面積は、 ( b - a ) x ( b - a ) = ( b - a ) 2 であることから、以下の関係式が成り立つ。 4 x 0.5ab + ( b - a ) 2 = c 2 この式を整理すると、 2ab + b 2 - 2ab + a 2 = c 2 a 2 + b 2 + 2ab - 2ab = c 2 a 2 + b 2 = c 2 |
 |
| 三平方定理の応用 |
| あ) 直角三角形の辺の長さ 直角三角形の2辺の長さがわかれば、残りの長さが求められる。 |
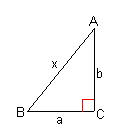
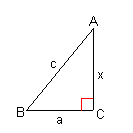
| 例1 | 例2 | ||
 |
 |
||
| x 2 = a 2 + b 2 より、 x = ( a 2 + b 2 ) 1/2 |
a 2 + x 2 = c 2 より、 x = ( c 2 - a 2 ) 1/2 |
| ※ 1/2乗とは、ルートのことです。 |
| い) 特殊な直角三角形の3辺の比 |
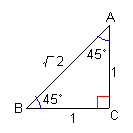
| 直角二等辺三角形の辺の比は、 1 : 1 : 21/2 |
鋭角が30°、60°の直角三角形の3辺の比は、 1 : 2 : 31/2 |
||
 |
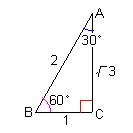 |
| う) 平面図形への応用 | |
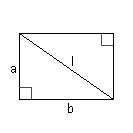
| 右図において、隣り合う2辺の長さが
a、bである長方形の対角線 l は、 l = ( a2 + b2 ) 1/2 また、1辺が長さ a である正方形の対角線の長さ l は、 l = ( 2a2 ) 1/2 = ( 2a ) 1/2 |
 |
| え) 座標平面上の2点間の距離 | |
| 2点 P(x1 , y1)、Q(x2 , y2)間の距離dは、 [ ( x2 - x1) 2 + ( y2 - y1) 2 ] 1/2 |
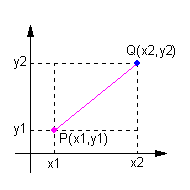 |
| お) 接線の長さ | |
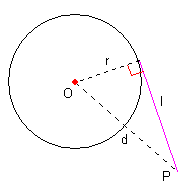
| 半径r の円の中心からの距離がd である点から引いた、接線の長さ l は、 l = ( d2 - r2 ) 1/2 |
 |
| ←前(図形の性質)へ | ここ(三平方の定理) | →次(立体の名称と特徴)へ |
| ▲このページトップへ |
| Copyright(C) KinutaHandicraft |