| ■適当講座■ 9.花子でCAD −図形の基礎− |
| a.図形の名称と特徴 | b.図形の各部の名称 | c.図形の性質 | d.三平方の定理 |
| e.立体の名称と特徴 | f.三角関数 | g.多面体 | h.曲面 |
| i.陰影 | j.透視 | k.角のn等分法 | l.曲線と直線 |
| c.図形の性質 |
| 図形の基本的な性質を理解しておくことは、作図に不可欠です。 | |
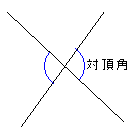
| 対頂角 対頂角の大きさは互いに等しい。 |
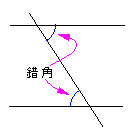
錯角 錯角が等しい2つの線分は平行である。 |
三角形の内角の和 三角形の内角の和は180°である。 |
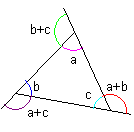
三角形の外角 三角形の外角は、それと隣り合わない2つの内角の和に等しい。 |
||||
 |
 |
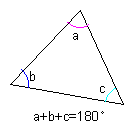 |
 |
| 比例 2つの長さの割合を、長さの比という。一方の比が他方の比と等しいことを比例という。 |
||||
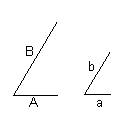 |
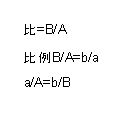 |
|||
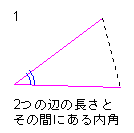
| 三角形の合同条件 三角形は、2つの辺の長さとその間にある内角、または1つの辺とその両端の2つの内角の 大きさ、または3つの辺の長さで決まる。 これらの等しい2つの三角形は互いに合同であるという。 |
|
 |
 |
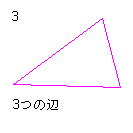 |
| 三角形の相似条件 1つの図形を、形を変えずに拡大または縮小するとき、その図形ともとの図形は 相似であるという。 2つの三角形が相似であるとき、その対応する内角はそれぞれ等しく、 対応する辺の長さは比例する。 |
|
|
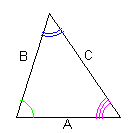 |
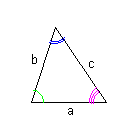 |
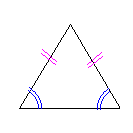
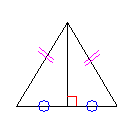
| 二等辺三角形 二等辺三角形の2つの底角の大きさは等しい。 |
二等辺三角形の頂角の2等分線は、底辺を直角に2等分する。 |
||
 |
 |
| 正三角形 正三角形の3つの内角の大きさはすべて等しく、3辺の長さも等しい。 |
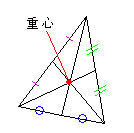
三角形の重心 三角形の3つの頂点から下した3つの中線は1てんで交わる。 この点を三角形の重心という。 |
多角形の内角の和 多角形(n角形)の内角の和は、180°x ( n - 2 )である。 |
|||||
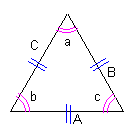 |
a = b = c = 60° A = B = C |
 |
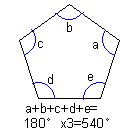 |
||||
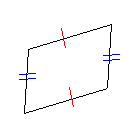
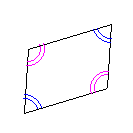
| 平行四辺形 平行四辺形の向かい合う辺の長さは等しい。 |
平行四辺形の向かい合う内角の大きさは等しい。 |
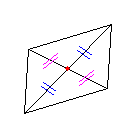
平行四辺形の対角線はそれぞれの中点で交わる。 |
|||
 |
 |
 |
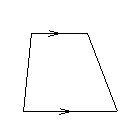
| 台形 1組の対辺が平行である四角形。 |
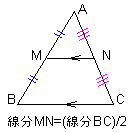
三角形の中点 三角形ABCの2辺の中点(M及びN)を結ぶ線分は、残りの辺に平行で、長さが半分となる。 |
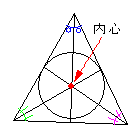
三角形の内心 三角形に内接する円の中心を内心という。 内心は、三角形の3つの内角の2等分線の交点である。 |
|||
 |
 |
 |
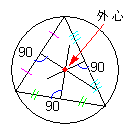
| 三角形の外心 三角形に外接する円の中心を外心という。 三角形の3つの辺の垂直2等分線の交点である。 |
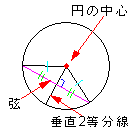
円 円の中心は弦の垂直2等分線上にある。 |
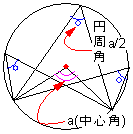
1つの弧に対する円周角はすべて等しく、その弧に対する中心角の半分である。 |
|||
 |
 |
 |
|||
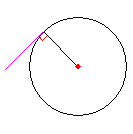
| 円(続き) 円の接線は、接点を通る半径に垂直である。 |
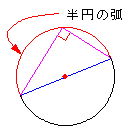
半径の弧に対する円周角は直角である。 |
円に内接する四角形の1組の向かい合う角の和は180°である。 |
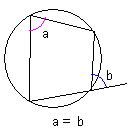
円に内接する四角形の1つの内角は、向かい合う内角の外角に等しい。 |
||||
 |
 |
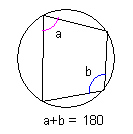 |
 |
| ←前(図形の各部の名称)へ | ここ(図形の性質) | →次(三平方の定理)へ |
| ▲このページトップへ |
| Copyright(C) KinutaHandicraft |