*
■適当講座■
*
10.花子で立体図　２軸回転体の作図

１／４     ２／４     ３／４     ４／４

☆ＸＺ軸回転体の作図(ＺＸ軸回転体の作図)　１／４
花子3.1まででは、拡大縮小点の自由度が大きかったので、 ＹＺ回転体やＸＹ回転体と同じ方法で、立体図を描けましたが、花子９以上では、 拡大縮小点の自由度が小さくなったので、ここでは、ＹＺ回転体やＸＹ回転体の 作図と整合性を持たせるため、ちょっと複雑なことをしています。
２軸回転体の性質を見ていただければ、もっと簡単にＸＺ回転体を描けます。

描く立体の元図は一辺を24.5mmの立方体とします。
描く立体は、Ｘ軸に１５°、Ｚ軸に２５°回転したものとします。
描く立体の基本諸元値を計算します。
    軸線長さ　24.5mm x 0.8165 = 20.0mm
    軸線の実角　３０°、９０°、１５０°
    楕円長軸　24.5mm
    楕円短軸　24.5 x 0.5774 = 14.1mm
各諸元値を求めたので、軸線・楕円を描きます（図2J-XZ01左）。
楕円は横長の楕円（Ｙ楕円）を描き、楕円の中心を出す意味で、楕円中心から、 垂線を引いておきます。
Ｙ楕円を元図残すで６０°、１２０°回転して、Ｘ楕円、Ｚ楕円にします。
一応、軸線を組み上げておきます（図2J-XZ01右）。
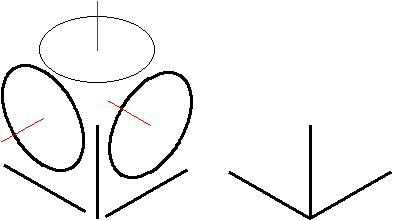図XZ回転体０１
図2J-XZ01　基本要素の作成

Ｘ楕円を軸線端点にコピーし、拡大します(図2J-XZ02)。
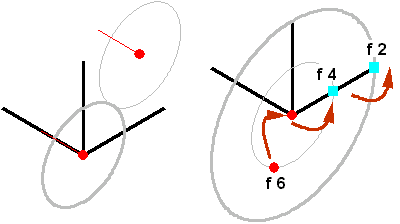図XZ回転体０２
図2J-XZ02　回転線範囲の楕円線の作成１

Ｚ楕円を軸線端点にコピーし、拡大します(図2J-XZ03)。
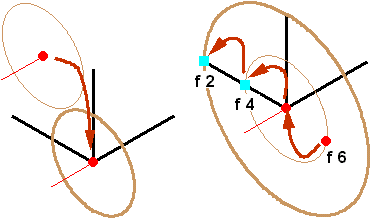図XZ回転体０３
図2J-XZ03　回転線範囲の楕円線の作成２

Ｙ軸（９０°）線、Ｚ軸（３０°）線を描き、十字にしておきます。 拡大したＸ楕円の中心が十字の交点に重なるようにＸ楕円を移動します。
Ｘ楕円分度器を用意し、Ｘ軸に１５°回転した線を作図します(図2J-XZ04。
次の十字に回転した線を移動します(図2J-XZ04)。
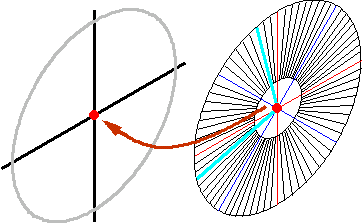図XZ回転体０４
図2J-XZ04　回転体作図開始

十字の交点を目標に回転線を載せます(図2J-XZ05左)。
その後、９０°線を図2J-XZ05右のようにコピーします。
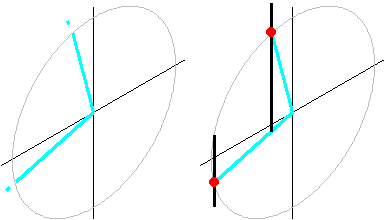図XZ回転体０５
図2J-XZ05　回転体作図開始

Ｚ楕円の端点から端点指定で線を２本引きます(図2J-XZ06左)。
それぞれの線を移動します(図2J-XZ06右)。
移動開始点を線の中点（ｆ３）としてして、移動終点を楕円端点（ｆ２）にします。
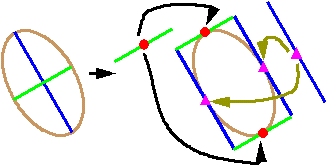図XZ回転体０６
図2J-XZ06　拡大縮小出来ない対策１

１／４     ２／４     ３／４     ４／４

▲このページトップへ

Copyright(C) KinutaHandicraft