■適当講座■

10.花子で立体図　１軸回転体の作図

☆Ｙ軸回転体の作図

	一辺24.5mmの正方形でＹ軸に２０°回転した立体を作図します。 計　算     一辺の長さ　24.5mm x 0.8165 = 20.00 = 20.0mm     楕円長軸長さ　24.5mm     楕円短軸長さ　24.5 x 0.5774 = 14.14 = 14.1mm 計算を元に線と楕円を作図し、組み上げておきます（図1J-Y01 左）。 さらに、Ｙ面の中心を出すために線を引きます（図1J-Y01 左の緑線）。 楕円をコピーします（図1J-Y01 右）。 楕円の中心をコピー中心にして、緑線の中点を移動終点にします。

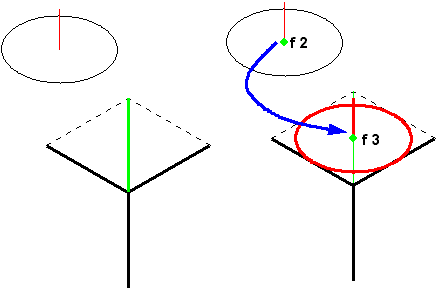図1J-Y01　Ｙ軸回転体の作図１

	楕円を移動します（図1J-Y02 左）。 楕円の中心を移動中心点として、面の角を移動終点とします。 楕円を拡大します（図1J-Y02 右） 。 楕円の中心を拡大中心として、楕円とＺ軸線の交点を拡大点として、Ｚ軸の端点を移動終点にします。 拡大した楕円の円周内が、回転した軸線の長さになります。

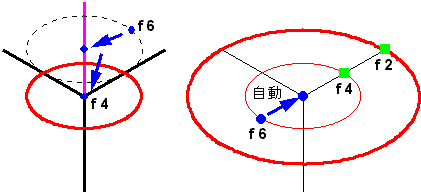図1J-Y02　Ｙ軸回転体の作図２

	楕円分度器を使って、２０°回転した軸線を作ります（図1J-Y03）。

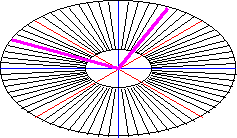図1J-Y03　Ｙ軸回転体の作図３

	回転した軸線を元図のＹ軸線の端点に移動します（図1J-Y04）。 拡大した楕円より回転した軸線が、長い場合、交点削除（交点消去）で軸線の長さを整えます。 回転した軸線が楕円円周より短い場合、図形情報で軸線の長さを長くします。

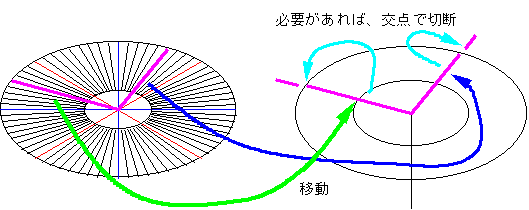図1J-Y04　Ｙ軸回転体の作図４

	回転した軸線の長さ−図形情報から、その軸線に対応する楕円の楕円比を求めます（図1J-Y05）。

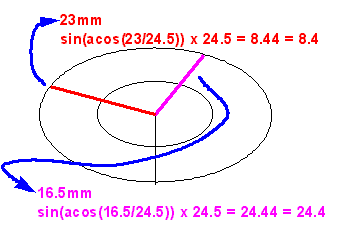図1J-Y05　Ｙ軸回転体の作図５

	長軸24.5mm−幅で、求めた短軸比−高さを持つ楕円を作り、楕円中心を出しておくために、 楕円の中心から垂線を引いておきます（図1J-Y06）。

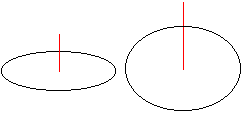図1J-Y06　Ｙ軸回転体の作図６

	求めた回転軸線の長さから、楕円比を求めるのが大変な場合、次の方法を使います。 数値表の楕円分度器諸元値を使う。 楕円を合わせるを参考にする。 回転した軸線とＹ軸線を立体図に組み上げます（図1J-Y07）。

図1J-Y07　Ｙ軸回転体の作図７

	各面の中心を出すために、線を引きます（図1J-Y08 左）。 取りあえず、Ｙ面にＹ楕円を移動します（図1J-Y08 右）。

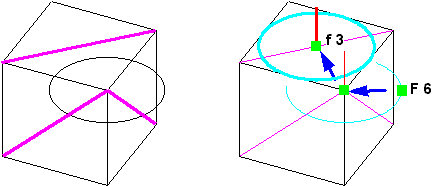図1J-Y08　Ｙ軸回転体の作図８

	Ｘ・Ｚ面の中心（線の中点）に各軸線の端点を移動点として、コピーします（図1J-Y09）。

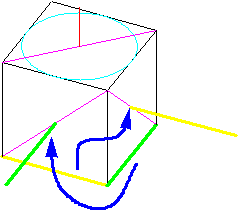図1J-Y09　Ｙ軸回転体の作図９

	Ｘ・Ｚ楕円とそれぞれの中心を指定して、移動中心を楕円の中心として、 中心を出した線の中点を移動終点として、移動します（図1J-Y10）。

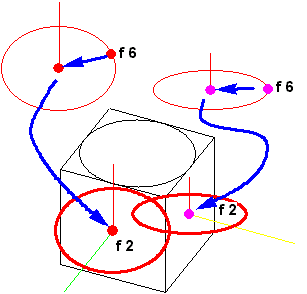図1J-Y10　Ｙ軸回転体の作図10

	楕円の回転（図1J-Y11） 楕円の中心を回転中心として、楕円と垂線の交点（ｆ４）で回転して、軸線上（ｆ５）で回転をやめます。

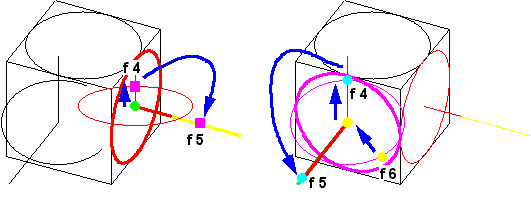図1J-Y11　Ｙ軸回転体の作図11

	余分な線を消したり、線種を変更して出来上がりです（図1J-Y12）。

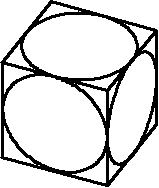図1J-Y12　Ｙ軸回転体の作図12

	▲このページトップへ

Copyright(C) KinutaHandicraft