キヌタハンディクラフト　適当講座　花子で立体図

■適当講座■

10.花子で立体図　等角投影図基本


	等角投影図を基本図として回転体を描く方法を考えますので、まず、座標系を明確にして関連する用語を定義し、次に等角投影図の描き方、その後、回転体を描くときに必要な楕円分度器の作成について見ていきます。

基本１　座標系について


	まず、座標軸と回転方向や回転角度（分度器角）を図１１の様にします。 ※平面図で示されている回転角度は円分度器で示されるのに対して、立体図の回転角度は楕円分度器で示される数値になります。


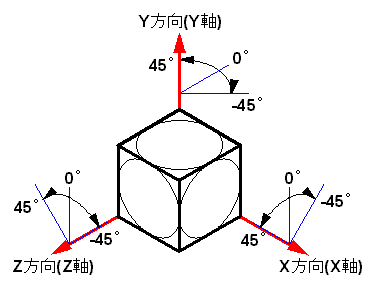	図１１　座標の決定

立体図を構成する線や楕円の名称は図１２の様にします。

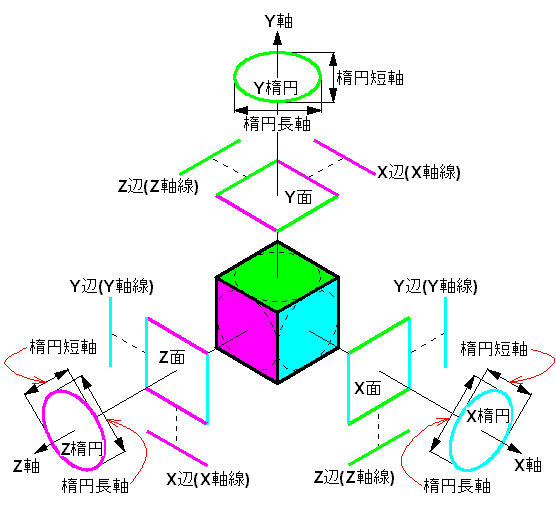図１２　立体図各部の名称

	楕円長軸を１としたときの楕円短軸の長さの比を楕円比とします。例：楕円比が0.3のとき、平面図の円の直径が30mmで、これを楕円長軸の１とします。

	1 : 0.3 = 30 : 楕円短軸楕円短軸 = 30 x 0.3 = 9mm

	平面図の一辺の長さを１としたとき、立体図にした平面図に対応する一辺（ある軸線）の長さの比を縮み率とします。例：縮み率が0.5のとき、平面図の一辺の20mmを１とします。

	1 : 0.5 = 20 : 求める値求める値 = 20 x 0.5 = 10 mm

各軸線を描くには、円分度器を使って軸線の角度を決めることになります。
各軸線の角度を実角とします（図１３）。

図１３　立体図各部の名称

今、長さが同じで、実角１５０°の線と実角３３０°（－３０°）の線を描いた場合、２本の線は完全に重なります（図１４参照）。
２つの線の実角の差は、１８０°なので、実角表記は、０°～１８０°の範囲で良いことが分かります。
つまり、０°の線を軸線のどの端点と合わせるかで、実角の差が１８０°になります。
また、実角のマイナス表記は作図上必要ありません。

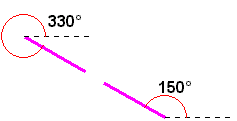図１４　実角が違う２本の線

→基本図を描くへ


	▲このページトップへ