キヌタハンディクラフト　適当講座　花子で立体図

■適当講座■

10.花子で立体図　数値表を使った作図の例-１軸回転体

各回転体諸元値表の見方について

	回転角度は各表の左側になります。縮み率は、平面図の各長さを１としたときの値になっています。そこで、立体図の構成要素（線）の長さは、　　平面図寸法　×　縮み率となります。実角は下図の通りです。
	図mlg-01　諸元値表の実角について

楕円比は、長軸を１としたときの短軸の比です。
そこで、立体図用の楕円の長軸・短軸は次の通りです。
長　軸　＝　図面寸法
短　軸　＝　楕円比　Ｘ　図面寸法
楕円と面を合わせるには、１軸回転体や２軸回転体の作図を参照してください。
楕円比の短軸が０の場合、線になるので、楕円の作図は必要ありません。

	例-Z25回転体を数値表を使って作成する
	まず、Z軸回転体諸元値表のZ分度器角度25の行の数値を取り出します。 0.4614 177.8度 0.9602 108.1度 0.8165 30.0度 0.7672 / 0.2792 / 0.5774

今、1.000を25mmとして計算します。
    0.6414 x 25 = 16.04 = 16.0mm/177.8度[黒色直線]
    0.9602 x 25 = 24.00 = 24.0mm/108.1度[茶色直線]
    0.8165 x 25 = 20.41 = 20.4mm/30.0度[黄土色直線]
    0.7672 x 25 = 19.18 = 19.2mm(高さ)/25.0mm(幅)[楕円]
    0.2792 x 25 = 6.98 = 7.0mm(高さ)/25.0mm(幅)[楕円]
    0.5774 x 25 = 14.43 = 14.4mm(高さ)/25.0mm(幅)[楕円]

	適当に直線３本と楕円３個を描き、図形情報に前記数値を入力します。楕円は、中心からの垂線を引いておきます(図zz101参照)。
	図zz101　基本線、基本楕円

	線をコピーしてくみ上げ、立体図にし(図zz102左参照)、各面の中心を通る線を引きます(図zz102左参照)。
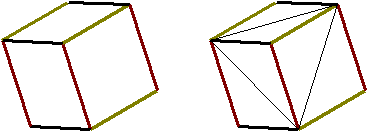	図zz102　基本立体図

	各面の通る線の中点に各軸線[直線]をコピーします。その後、楕円を面中心に移動し(図zz103左)、回転します(図zz103右)。
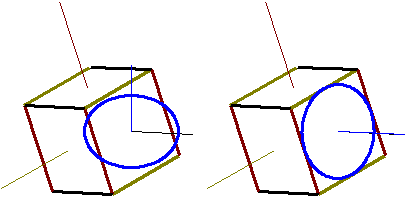	図zz103　面に楕円を合わせる

	その後、他の面にも楕円を移動して回転し(図zz104左)、余分な図形を消して完成です(図zz104右)。
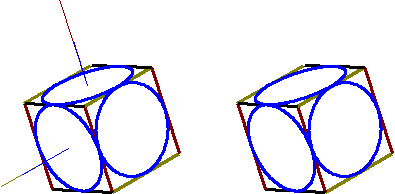	図zz104　Z25回転体の完成

中心からの垂線、面中心に楕円を合わせる、楕円を回転するなどのテクニックでは、ファンクションキーを多用しております。
これらのテクニックの詳細につきましては、数値表を使わない１軸回転体の作図を見てください。

▲このページトップへ