*
■適当講座■
*
10.花子で立体図　１軸回転体の作図

☆１軸回転体の性質（？）
先ず、Ｙ軸回転体を０°から９０°まで作図しています（図1J-S01）。
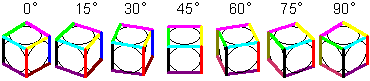１軸回転体の性質１
図1J-S01　Ｙ軸回転体の性質１
４５°回転体（以後Y45）中心にして左右を見ると左右の図形はミラー の関係にあることがわかります。
Ｙ０とＹ９０は、 全く同じ諸元値を持つことが、分かります（図1J-S01）。
よって、１軸回転体はY−４５°からY４５°の範囲が分かっていればいいことになります。
最低限必要な諸元値はY０°からY４５°までになり、残りは、ミラー処理で補えます。
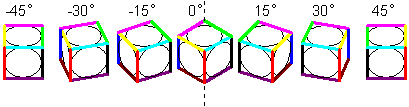１軸回転体の性質２
図1J-S02　Ｙ軸回転体の性質２
Ｙ軸回転体をまとめると、
→Ｙ軸回転体を９０°線でミラー（左右のミラー）をかけると、符号の反転したＹ軸回転体になります。

Ｘ軸回転体を考えてみると、Ｙ楕円分度器を６０°回転したものが、Ｘ楕円分度器ですから、 Ｙ軸回転体を６０°回転させると、上下が逆さまになってしまします。
そこで、さらに１８０°回転させると、上下の合ったＸ軸回転体になります（図1J-S03）。
１軸回転体の性質３
１軸回転体の性質３補足

図1J-S03　Ｙ軸回転体を２４０°回転させたＸ軸回転体
Ｘ軸回転体の性質のまとめ
→Ｘ回転体を１５０°線でミラーすると符号が反転したＸ軸回転体になります。
→Ｙ軸回転体を２４０°回転すると、Ｘ軸回転体になります。
→Ｘ軸回転体を９０°線でミラー（左右にミラー）すると、符号の反転したＺ軸回転体になります。

Ｚ軸回転体を考えると、Ｙ軸楕円分度器を１２０°回転させて、Ｚ軸楕円分度器を作ったので、 Ｙ軸回転体を１２０°回転させれば、Ｚ軸回転体になります（図1J-S04）。
１軸回転体の性質４
１軸回転体の性質４補足

図1J-S04　Ｙ軸回転体を１２０°回転させたＺ軸回転体
Ｚ軸回転体の性質
→Ｙ軸回転体を１２０°回転するとＺ軸回転体になります。
→Ｚ軸回転体を３０°線でミラーすると符号の反転したＺ軸回転体になります。
→Ｚ軸回転体を９０°線でミラー（左右にミラー）すると、符号の反転したＸ軸回転体になります。

▲このページトップへ

Copyright(C) KinutaHandicraft