*
■適当講座■
*
10.花子で立体図　等角投影図へ４　等角投影図
等角図と上面図から視野の角度を求めるための図形、図８を描き、視野の角度を求めてみます。
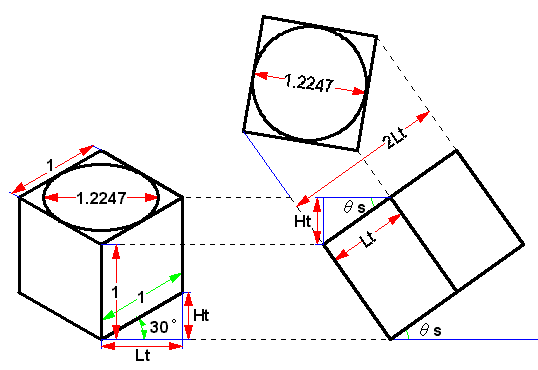視野角を求めるための等角図の作図
図８　視野の角度を求めるための作図

視野の角度の計算は次のようになります。

　　Cos30deg = Lt/1 → Lt = 0.866

　　Sin30deg = Ht/1 → Ht = 0.5

　　Sinθs = Ht/Lt = 0.5 / 0.866 = 0.5774 → θs = 35.2667 = 35度16分

等角図の”視野の角度”は３５゜１６’であることが分かりました。

図８からの作図でも分かるように、等角図（立体図）から平面図を描く場合、元の寸法の何倍かしたものになり、 いつも平面図と立体図をセットで持ち歩かなければなりません。

もし、一度立体図が完成したら、立体図だけから必要に応じて、平面図を簡単に描ければ、大変便利です。

そこで、視野の角度も分かっているので、平面図を組み合わせて、立体図を描く方法を確立すれば、立体図から、 等倍の平面図が描けるはずです。

では、さっそく等倍の平面図から立体図を図９の通り作図します。

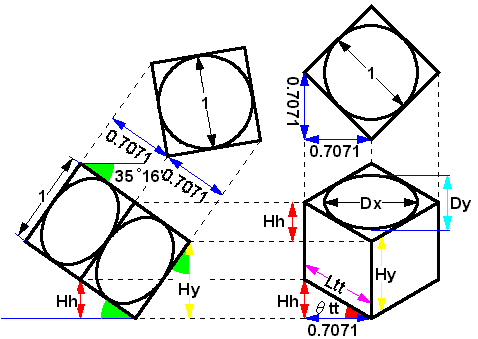平面図からの立体図
図９　諸元値を出すための作図（２）

作図出来たので、図９を元に諸元値を計算してみます。

△θtt、Lttを求める
　　Sin 35deg16min. = Hh / 0.7071 → Hh = 0.7071 x 0.5774 = 0.4083
　　Tan θtt = Hh / 0.7071 = 0.5774 → θtt = 30deg
　　Cos 30deg = 0.7071 / Ltt → Ltt = 0.7071 / Cos 30deg = 0.8165

△Hyを求める
　　Cos 35deg16min. = Hy / 1 → Hy = 0.8165

△Dx、Dyを求める
　　Dx = 1
　　Dy = 1 x (Hh / 0.7071 ) = 1 x ( 0.4083 / 0.7071 ) = 0.5774

求めた諸元値を図１０にまとめてみます。

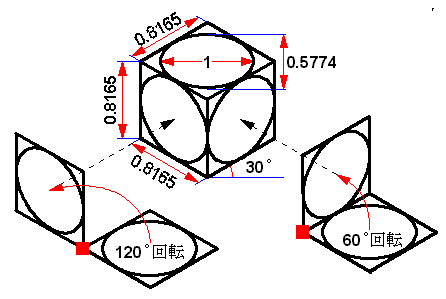等角投影図の諸元値
図１０　？図の諸元値

図１０の諸元値を持つ立体図を等角投影図といいます。

以後、図１０の等角投影図を0ﾟ回転体とし、１軸回転体・２軸回転体の描き方を考えていきます。
* *
▲このページトップへ
Copyright(C) KinutaHandicraft