*
■適当講座■
*
10.花子で立体図　等角投影図へ２　等角図
・見た目の歪みを小さくするためには、 三辺が等角で交わりようにするすればよいです。
つまり、
　　　　　３６０÷３＝１２０
と三辺の長さが等倍で、交わる角度がそれぞれ１２０度になる立体図を描けばよさそうです。
・各辺(線)の長さを１として、描いた立体図は、図３です。

・図３の立体図は見た目の歪みも少なく、立方体に見えるではありませんか！

・各辺の長さは、１で、各辺の角度もわかっているので、あとは円の大きさを知りたいです。
そこで、立体図の上面の楕円の大きさを求めてみます。
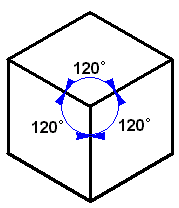※補助として、平面図の上面図を描いておきます。		 線が等角で交わる立体図
図３　三辺が等角で交わる立体図
・最終的に求めたいのは、Ytです。

　　Cos30deg = Lt/1　→　Lt = 0.866

　　Sin45deg = Xt/0.866　→　
　　Xt = 0.866/0.7071 = 1.2247

　　Sin30deg = Ht/1　→　Ht = 0.5

　　Yt = Xt(2Ht/2Xt) = 1.2247x(0.5/0.866) =
　　0.7071

となり、線の長さを１としたときの各数値の比（諸元値）は、図５の通りです。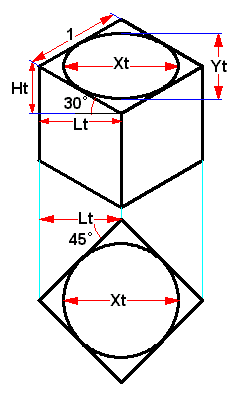
立体図の諸元値を出すための作図
図４　諸元値を出すための作図（１）
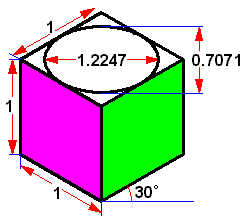等角図諸元値−未完
図５　見ために立方体に見える図形の諸元値
・今、図５の立体図の上面の諸元値は決定しましたが、緑色面とピンク色面の楕円はどのようになるのでしょうか？

上面と各面を合わせてみると、上面を回転することで、緑色面とピンク色面の楕円が描けそうです。

上面を色々回転した結果、緑色面は上面を60deg回転したものであり、また、ピンク色面は上面を120deg回転したものであることが分かります （図６参照）。
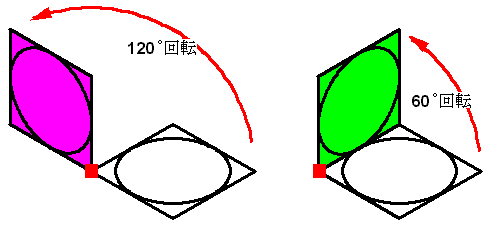等角図の側面と上面の関係
図６　上面図と側面図の関係
・先程の諸元値を持つ立体図を等角図といいます。

次に、等角図は図形の投影結果なので、元の図形をどのように見ているかを知りたいです。

結論としては、視野の角度を考えればいいことになります。

つまり、見た目の角度は視野の角度（本内容では”視野角”と言う場合がある）といわれ、次に視野の角度について考えてみます。　→　視野の角度　へ
* *
▲このページトップへ
Copyright(C) KinutaHandicraft